I. Pengertian Statistika dan Data
Statistika adalah ilmu pengetahuan yang mempelajari tentang mengumpulkan, menyusun, mengolah, menganalisis, menyimpulkan, dan menyajikan data hasil penelitian. Sementara statistik adalah data hasil olahan dan analisis.
Data (bentuk jamak) adalah keterangan suatu obyek yang diteliti. Sementara datum (bentuk tunggal) adalah keterangan suatu obyek yang diteliti. Data terbagi menjadi dua, yaitu data Numerik (kuantitas) dan data Kategori (kualitas. Data numerik adalah data berupa hasil pengukuran atau penghitungan. Sementara data kategori adalah data yang bukan berupa angka. Pengumpulan data dilakukan dengan:
- Mencacah/menghitung
- Mengukur
- Mengunakan tally atau turus
Populasi dan Sampel
Populasi adalah keseluruhan obyek yang memiliki karakteristik (sifat) sama yang akan diteliti.
Sampel adalah bagian dari populasi yang dapat mewakili keadaan yang benar mengenai populasi yang diteliti.
TENDENSI SENTRAL (Ukuran Pemusatan)
- Rata-rata hitung (Mean)
- Modus
- Median
CONTOH:
Data: 162,160, 170, 165, 167, 170, 165
Mean => Rata-rata hitung
ex:n=162+160+170+165+167+170+165:7
=1159:7=165.57
Modus =>Nilai yang sering muncul
CONTOH:
Data: 160, 162, 165, 165, 167, 170, 170
Modusnya adalah 165 dan 170
Median => Nilai tengah setelah data diurutkan
CONTOH:
Data terurut: 160, 162, 165, 165, 167, 170, 170
Mediannya adalah 165
Mean dalam tabel frekuensi
CONTOH:
Nilai 5 6 7 8 9 10 Frekuensi 3 6 5 17 5 4
Mean
= e(f.x):e.f= 3(5) + 6(6) + 5(7) + 17(8) + 5(9) + 4(10):3 + 6 + 5 + 17 + 5 + 4
= 15 + 36 + 35 + 136 + 45 + 40:40 = 307:40
=7,675
Ukuran Pemancaran Data Tunggal
- Range (jangkauan data)
- Quartil
- Jangkauan Quartil
- Jangkauan Interquartil
- Simpangan Quartil
- Range (jangkauan data)
- Data tertinggi - Data terendah
- Quartil = Q
- Pembagi data menjadi 4 bagian sama banyak Q1, Q2, Q3 Q2= Median
- Jangakuan Quartil = Jangkauan Interquartil
- Q3 - Q1
- Simpangan Quartil
- Q3 - Q1:2
Penyajian Data
- Menyajikan data
- Membaca/menafsirkan data
Penyajian data divisualisasikan melalui:
- Piktogram/lambang/gambar
- Diagram batang
- Diagram garis
- Diagram lingkaran
II. Peluang
Peluang disebut juga probabilitas yang berarti ilmu kemungkinan. Di dalam peluang dikenal ruang sampel dan titik sampel.
Ruang sampel adalah himpunan semua hasil/kejadian yang mungkin terjadi dan dilambangkan dengan S
Peluang (P) =Banyak kejadian muncul/Banyak kejadian yang mungkin
Contoh: P=400/1200 = 1/3
Komplemen dari nilai di atas = 1200-400:1200
=800/1200 = 2/3
Frekuensi nisbi = Banyak Kejadian Muncul/Banyak percobaan
Frekuensi harapan = Banyak percobaan x Peluang
Ruang sampel dan Titik Sampel
Ruang sampel adalah himpunan semua hasil/kejadian yang mungkin terjadi dan dilambangkan dengan S.
Dalam beberapa peercobaan, ruang sampel dapat ditentukan dengan menggunakan diagram pohon maupun tabel, dan anggota-anggota ruang sampel dapat didaftar secara mudah dan teratur.
Pengetosan Dua Mata Uang
A G A (A,A) (A,G) G (G,A) (G,G)
Banyak titik sampel= 2x2 = 4
Pengetosan Dua Dadu
1 2 3 4 5 6 1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6) 2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6) 3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6) 4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6) 5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6) 6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
Banyak titik sampel = 6x6 = 36
Pengetosan Mata Uang dan Dadu
1 2 3 4 5 6 A (A,1) (A,2) (A,3) (A,4) (A,5) (A,6) G (G,1) (G,2) (G,3) (G,4) (G,5) (G,6)
Banyak titik sampel = 2x6 = 12
Statistika adalah ilmu pengetahuan yang mempelajari tentang mengumpulkan, menyusun, mengolah, menganalisis, menyimpulkan, dan menyajikan data hasil penelitian. Sementara statistik adalah data hasil olahan dan analisis.
Data (bentuk jamak) adalah keterangan suatu obyek yang diteliti. Sementara datum (bentuk tunggal) adalah keterangan suatu obyek yang diteliti. Data terbagi menjadi dua, yaitu data Numerik (kuantitas) dan data Kategori (kualitas. Data numerik adalah data berupa hasil pengukuran atau penghitungan. Sementara data kategori adalah data yang bukan berupa angka. Pengumpulan data dilakukan dengan:
- Mencacah/menghitung
- Mengukur
- Mengunakan tally atau turus
Populasi dan Sampel
Populasi adalah keseluruhan obyek yang memiliki karakteristik (sifat) sama yang akan diteliti.
Sampel adalah bagian dari populasi yang dapat mewakili keadaan yang benar mengenai populasi yang diteliti.
TENDENSI SENTRAL (Ukuran Pemusatan)
- Rata-rata hitung (Mean)
- Modus
- Median
CONTOH:
Data: 162,160, 170, 165, 167, 170, 165
Mean => Rata-rata hitung
ex:n=162+160+170+165+167+170+165:7
=1159:7=165.57
Modus =>Nilai yang sering muncul
CONTOH:
Data: 160, 162, 165, 165, 167, 170, 170
Modusnya adalah 165 dan 170
Median => Nilai tengah setelah data diurutkan
CONTOH:
Data terurut: 160, 162, 165, 165, 167, 170, 170
Mediannya adalah 165
Mean dalam tabel frekuensi
CONTOH:
| Nilai | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|
| Frekuensi | 3 | 6 | 5 | 17 | 5 | 4 |
Mean
= e(f.x):e.f= 3(5) + 6(6) + 5(7) + 17(8) + 5(9) + 4(10):3 + 6 + 5 + 17 + 5 + 4
= 15 + 36 + 35 + 136 + 45 + 40:40 = 307:40
=7,675
Ukuran Pemancaran Data Tunggal
- Range (jangkauan data)
- Quartil
- Jangkauan Quartil
- Jangkauan Interquartil
- Simpangan Quartil
- Range (jangkauan data)
- Data tertinggi - Data terendah
- Quartil = Q
- Pembagi data menjadi 4 bagian sama banyak Q1, Q2, Q3 Q2= Median
- Jangakuan Quartil = Jangkauan Interquartil
- Q3 - Q1
- Simpangan Quartil
- Q3 - Q1:2
Penyajian Data
- Menyajikan data
- Membaca/menafsirkan data
Penyajian data divisualisasikan melalui:
- Piktogram/lambang/gambar
- Diagram batang
- Diagram garis
- Diagram lingkaran
II. Peluang
Peluang disebut juga probabilitas yang berarti ilmu kemungkinan. Di dalam peluang dikenal ruang sampel dan titik sampel.
Ruang sampel adalah himpunan semua hasil/kejadian yang mungkin terjadi dan dilambangkan dengan S
Peluang (P) =Banyak kejadian muncul/Banyak kejadian yang mungkin
Contoh: P=400/1200 = 1/3
Komplemen dari nilai di atas = 1200-400:1200
=800/1200 = 2/3
Frekuensi nisbi = Banyak Kejadian Muncul/Banyak percobaan
Frekuensi harapan = Banyak percobaan x Peluang
Ruang sampel dan Titik Sampel
Ruang sampel adalah himpunan semua hasil/kejadian yang mungkin terjadi dan dilambangkan dengan S.
Dalam beberapa peercobaan, ruang sampel dapat ditentukan dengan menggunakan diagram pohon maupun tabel, dan anggota-anggota ruang sampel dapat didaftar secara mudah dan teratur.
Pengetosan Dua Mata Uang
| A | G | |
|---|---|---|
| A | (A,A) | (A,G) |
| G | (G,A) | (G,G) |
Banyak titik sampel= 2x2 = 4
Pengetosan Dua Dadu
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) |
| 6 | (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
Banyak titik sampel = 6x6 = 36
Pengetosan Mata Uang dan Dadu
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| A | (A,1) | (A,2) | (A,3) | (A,4) | (A,5) | (A,6) |
| G | (G,1) | (G,2) | (G,3) | (G,4) | (G,5) | (G,6) |
Banyak titik sampel = 2x6 = 12
Identitas trigonometri
Penjumlahan
Perkalian
Rumus sudut rangkap dua
Rumus sudut rangkap tiga
Rumus setengah sudut
Aturan Sinus, Cosinus, dan Tangen
Aturan sinus
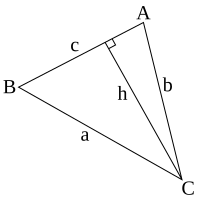
Turunan dari aturan sinus
Luasan dari segitiga diatas dapat dirumuskan sebagai
Kalikan persamaan diatas dengan  maka akan menjadi
maka akan menjadi
 maka akan menjadi
maka akan menjadi

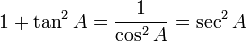

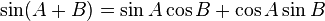
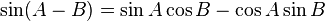
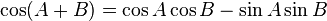

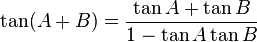
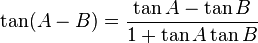
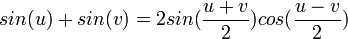

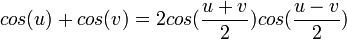
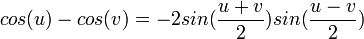



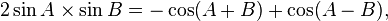

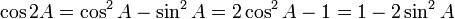




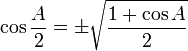
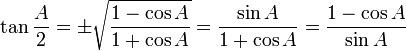

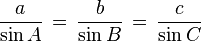
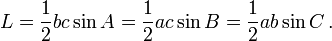
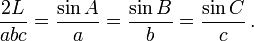

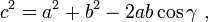
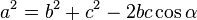

![\frac{a-b}{a+b} = \frac{\tan[\frac{1}{2}(\alpha-\beta)]}{\tan[\frac{1}{2}(\alpha+\beta)]}.](https://upload.wikimedia.org/math/c/3/4/c34b871436dbf7e3a62c5337536ab791.png)





